CbKST & FCA

One of the main aims of LEA’s BOX is to provide a competence-centred and non-invasive methodology for the assessment of the learning progress of individual learners as well as groups of learners. The notion of learning progress implies the change of a learner´s current state of knowledge, abilities, skills and competences over time. A valid assessment of such changes over time, or in other words, a valid and non-invasive assessment of learning by means of Learning Analytics, requires a precise and well-described representation of the learning domain. LEA´s BOX applies two psycho-pedagogically sound frameworks to describe the learning domain in a formalized and precise way: The Formal Concept Analysis and the (Competence-based) Knowledge Space Theory. Competence-based Knowledge Space Theory (CbKST) Another framework with a similar mathematical background, definitions, and objectives is the Competence-based Knowledge Space Theory which provides a theoretical framework for knowledge and competence modeling (Albert & Lukas, 1999; Falmagne & Doignon, 2011; Falmagne, Albert, Doble, Eppstein, & Hu, 2013). It is a powerful approach for structuring and representing domain and learner knowledge. In its original formalisation, a knowledge domain is characterized by a set of problems or test items. The knowledge state of an individual is identified with the subset of problems this person is able to solve. Due to mutual dependencies between the problems, not all potential knowledge states will occur. These dependencies are captured by the so-called prerequisite relation or its generalisation, the prerequisite function. The collection of all possible states is called a knowledge structure. Competence-based extensions of the original framework (Albert & Lukas, 1999; Heller, Ünlü, & Albert, 2013; Heller, Steiner, Hockemeyer, & Albert, 2006) consider the latent cognitive constructs underlying observable behaviour and assume a competence structure on a set of abstract skills underlying the problems and learning objects of the domain. By associating skills to the problems and learning objects of a domain, knowledge and learning structures on the problems and, respectively, learning objects are induced. The skills, which are not directly observable, can be uncovered on the basis of a person’s observable performance. Skills are thereby commonly defined adopting learning and teaching goals as they can be identified from the curriculum (Korossy, 1997) and by combining action/procedural and conceptual/declarative components (Marte, Steiner, Heller, & Albert, 2008). These skills can be related to existing educational taxonomies (e.g. Anderson & Krathwohl, 2001); the skill modelling approach of CbKST is therefore in line with approaches aiming at the standardised and comparable representation of competence as an outcome of educational programs or school types and at providing a supporting frame for competence-oriented and learner-centred instruction (e.g. BMUKK, 2012; European Communities, 2007, 2008; European Commission, 2012).    The structures CbKST formulates on skills (or problems) in terms of prerequisite relations or functions can be graphically depicted by Hasse diagrams (e.g. Pemmaraju & Skiena, 1990) and, respectively, And/Or graphs, which are directed graphs with the nodes representing the problems of a domain and the arcs representing prerequisite relationships among those problems. These structures are traditionally been used at the backend of learning technologies, as a basis for adaptation mechanisms. In the iClass project an approach of opening the structures on domain skills and their association with learning objects and assessment problems to end users has been taken. A range of visual tools has been developed to empower learners and teachers in planning and performing their learning and teaching, and to help them in reflecting on the learning and teaching process (Nussbaumer, Steiner, & Albert, 2008; Steiner, Nussbaumer, & Albert, 2009). In particular, one of these tools – in line with ideas of open learner models - visualises assessment results on skills and reports them back to learners (and teachers) to enable reflection on acquired skills and identification of existing competence gaps. CbKST provides the basis for adaptive assessment procedures of a learner’s current competence and knowledge state as well as for the realisation of intelligent educational adaptation and has been successfully applied as a cognitive basis for realising in terms of personalising learning experiences in different learning systems (Albert, Hockemeyer, & Wesiak, 2002; Conlan, O’Keeffe, Hampson, & Heller, 2006; Falmagne, Cosyn, Doignon, & Thiéry, 2006). The so-called microadaptivity approach (Augustin, Hockemeyer, Kickmeier-Rust, & Albert, 2011; Kickmeier-Rust & Albert, 2010) has been developed and applied in the context of game-based learning (Kickmeier-Rust, Mattheiss, Steiner, & Albert, 2011) and integrates CbKST with theory of human problem solving (Newell & Simon, 1972) in order to model learners’ behaviour and skills in problems solving during learning and assessment situations. The approach enables non-invasive assessment of learners’ available and lacking skills by monitoring and interpreting their (inter)actions in the learning environment during problem solving and the gathered assumptions on a learner’s skills serve the provision of adaptive hints, prompts or feedback tailored to the learner’s available and lacking skills (e.g. Kickmeier-Rust, Steiner, & Albert, 2011). Microadaptivity can therefore be understood as an approach to formative assessment and tailored educational interventions. Formal Concept Analysis (FCA) Formal Concept Analysis (FCA), established by Wille (1982), aims to describe concepts and concept hierarchies in mathematical terms. The starting point of the FCA is the specification of a “formal context” (also called learning domain). The formal context K is defined as a triple (G, M, I) with G as a set of objects which belong to the learning domain, M as a set of attributes which describe the learning domain, and finally, I as a binary relation between G and M. The relation I connects objects and attributes, i.e. (g, m) ∈ I means the object g has the attribute m. The formal context K can be best read when depicted as a cross table, with the objects in the rows, the attributes in the columns and relations between them by assigning “X” in the according cells. A formal concept is a pair (A, B) with A as a subset of objects and B as a subset of attributes. A is called the extension of the formal concept; it is the set of objects which belong to the formal concept. B is called the intension, it is the set of attributes which apply to all objects of the extension. 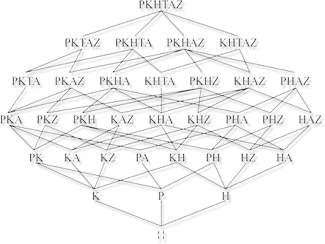The ordered set of all formal concepts is called the concept lattice B(K) (see Wille, 2005) Every node of the Concept Lattice represents a single formal concept. The extension of a particular formal concept can be read off from the lattice by gathering all objects which can be reached by descending paths from that node. The intension is represented by all attributes which can be reached by an ascending path from that node. For example, the node with the label “Leech” represents a formal concept with {Leech, Goldfish) as extension and {m1, m2} as intension. 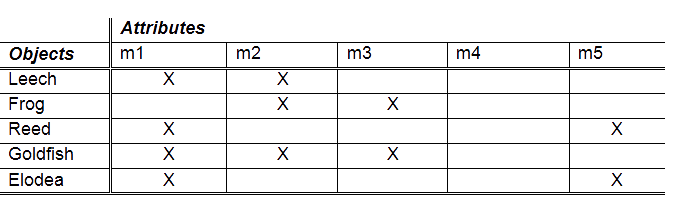Learning Domain Biotope (Formal Context based on Ganter and Wille, 1996)           Notes regarding attributes: m1…lives solely in the water, m2…is able to change location,           m3… has limbs, m4…breastfeeds descendants, m5…applies photosynthesis

References

lbert, D., Hockemeyer, C., & Wesiak, G. (2002). Current trends in eLearning based on knowledge space theory and cognitive psychology. Psychologische Beiträge, 44, 478-494.

Albert D. & Lukas J. (1999). Knowledge spaces: Theories, empirical research, applications. Mahwah: Lawrence Erlbaum Associates.

Albert, D., Nussbaumer, A. & Steiner, C.M. (2010). Towards Generic Visualisation Tools and Techniques for Adaptive E-Learning, In S.L. Wong et al. (Eds). International Conference on Computers in Education (pp. 61-65), Putrajaya, Malaysia, Asia-Pacific Society for Computers in Education.

Anderson, L.W. & Krathwohl, D.R (Eds.) (2001). A taxonomy for learning, teaching, and assessing: A revision of Bloom's taxonomy of educational objectives. New York: Longman.

Augustin, T., Hockemeyer, C., Kickmeier-Rust, M., & Albert, D. (2011). Individualized skill assessment in digital learning games: Basic definitions and mathematical formalism. IEEE Transactions on Learning Technologies, 4, 138-148.

BMUKK (2012). Kompetenzorientiertes Unterrichten an berufsbildenden Schulen. Grundlagenpapier [Competence-oriented instruction at vocational schools. White paper]. Wien: Bundesministerium für Unterricht, Kunst und Kultur.

Conlan, O., O'Keeffe, I., Hampson, C., & Heller, J. (2006). Using knowledge space theory to support learner modeling and personalization. In T. Reeves & S. Yamashita (Eds.), Proceedings of World Conference on E-Learning in Corporate, Government, Healthcare, and Higher Education (pp. 1912-1919). Chesapeake: AACE.

European Communities (2007). Key competencies for lifelong learning: European Reference Framework. Luxembourg: Office for Official Publications of the European Communities.

European Communities (2008). Explaining the European Qualifications Framework for Lifelong Learning. Luxembourg: Office for Official Publications of the European Communities.

European Commission (2012). Assessment of key competencies in initial education and training: Policy guidance. Commission staff working document. SWD(2012) 371. Strasbourg.

Falmagne, J.-C., Albert, D., Doble, C., Eppstein, D. & Hu, X. (Eds.) (2013). Knowledge spaces: Applications in education. New York: Springer.

Falmagne, J.-C., Cosyn, E., Doignon, J.P., & Thiéry, N. (2006). The assessment of knowledge, in theory and practice. In R. Missaou & J. Schmidt (Eds.), Formal Concept Analysis. 4th International Conference, ICFCA. Lecture Notes in Artificial Intelligence vol. 3874 (pp. 61-79). Berlin: Springer.

Falmagne, J.- C. & Doignon, J. P. (2011). Learning Spaces: Interdisciplinary Applied Mathematics. New York: Springer Verlag.

Fruhmann, K., Nussbaumer, A., & Albert, D. (2010). A Psycho-Pedagogical Framework for Self-Regulated Learning in a Responsive Open Learning Environment. Proceedings of the International Conference eLearning Baltics Science.

Ganter, B., & Wille, R. (1996). Formale Begriffsanalyse - Mathematische Grundlagen. Heidelberg: Springer Verlag.

Heller, J., Ünlü, A., & Albert, D. (2013). Skills, competencies, and knowledge structures. In J.-C. Falmagne, D. Albert, C. Doble, D. Eppstein, & X. Hu (Eds.), Knowledge spaces: Applications in education. Springer.

Heller, J., Steiner, C., Hockemeyer, C., & Albert, D. (2006). Competence-based knowledge structures for personalised learning. International Journal on E-Learning, 5, 75-88.

Kickmeier-Rust, M.D., & Albert, D. (in press). Using Hasse Diagrams for Competence-Oriented Learning Analytics. To appear in Springer LNCS.Kickmeier-Rust, M.D., & Albert, D. (2010). Micro adaptivity: Protecting immersion in didactically adaptive digital educational games. Journal of Computer Assisted Learning, 26, 95-105.

Kickmeier-Rust, M.D., Steiner, C.,M. & Albert, D. (2011). Apt to adapt: Micro- and macro-level adaptation in educational games. In T. Daradoumis, S. Caballé, A. Juan & F. Xhafa (Eds.), Technology-Enhanced Systems and Tools for Collaborative Learning Scaffolding. Studies in Computational Intelligence vol. 350 (pp. 221-238). Berlin: Springer.

Kickmeier-Rust, M.D., Mattheiss, E., Steiner, C.M., & Albert, D. (2011). A psycho-pedagogical framework for multi-adaptive educational games. International Journal of Game-Based Learning, 1. 45-58.
Korossy, K. (1997). Extending the theory of knowledge spaces: a competence-performance approach. Zeitschrift für Psychologie, 205, 53-82.

Kopeinik, S., Nussbaumer, A., Bedek, M., Albert, D. (2012). Using CbKST for Learning Path Recommendation in Game-based Learning. In Proceedings of the 20th International Conference on Computers in Education (pp. 86 – 91), ICCE 2012.

Marte, B., Steiner, C.M., Heller, J., & Albert, D. (2008). Activity- and taxonomy-based knowledge representation framework. International Journal of Knowledge and Learning, 4, 189-202.

Newell A. & Simon H. (1972) Human problem solving. Englewood Cliffs, NJ: Prentice-Hall.

Nussbaumer, A., Steiner, C., & Albert, D. (2008). Visualisation tools for supporting self-regulated learning through exploiting competence structures. In K. Tochtermann, H. Maurer, F. Kappe, & W. Haas (Eds.), Proceedings of I-KNOW’08 and I-MEDIA’08. International Conferences on Knowledge Management and New Media Technology (pp. 288-295). Graz: J.UCS.

Papanikolaou, K. & Grigoriadou, M. (2003). Adaptive web-based learning: accommodating individual differences through system’s adaptation. British Journal of Educational Technology, 34(4), 511 -527.

R usch, A., & Wille, R. (1996). Knowledge spaces and formal concept analysis. In H. H. Bock & W. Polasek (Eds.), Data analysis and information systems: Statistical and conceptual approaches (pp. 427-436). Berlin: Springer.

Ünlü, A., Schrepp, M., Heller, J., Hockemeyer, C., Wesiak, G., & Albert, D. (2013). Recent developments in performance-based knowledge space theory. In J.-C. Falmagne, D. Albert, C. Doble, D. Eppstein, & X. Hu (Eds.), Knowledge spaces: Applications in education. New York: Springer.

Wille, R. (1982). Restructuring lattice theory: An approach based on hierarchies of concepts. In I. Rival (Ed.), Ordered sets (pp. 445–470). Dordrecht: Reidel.

Wille, R. (2005). Formal Concept Analysis as Mathematical Theory of Concepts and Concept Hierarchies, In B. Ganter , G. Stumme and R. Wille (Eds.), Formal Concept Analysis (pp. 1-34), Berlin: Springer.